使用张量表达式处理算子
导航
使用张量表达式处理算子#
Author: Tianqi Chen
在本教程中,把注意力转向 TVM 如何使用张量表达式(Tensor Expression,简称 TE)定义张量计算并应用循环优化。TE 以纯函数式语言描述张量计算(即每个表达式都没有副作用)。从 TVM 的整体来看,Relay 将计算描述为一组算子,这些算子都可以表示为 TE 表达式,每个 TE 表达式都接受输入张量并生成输出张量。
这是关于 TVM 中张量表达式语言的介绍性教程。TVM 使用领域专用张量表达式来进行有效的内核构建。通过两个使用张量表达式语言的例子,演示基本工作流程。第一个例子介绍了 TE 和用向量加法进行调度。第二个例子扩展了这些概念,用 TE 逐步优化矩阵乘法。这个矩阵乘法的例子将作为未来涵盖 TVM 更高级功能的教程的基础。
例 1:为 CPU 编写和调度 TE 中的向量加法#
让我们看看 Python 中的例子,将实现向量加法的 TE,然后是针对 CPU 的调度。首先初始化 TVM 环境。
import warnings
import numpy as np
# import env
import tvm
from tvm import testing
from tvm import te
from tvm.target import Target
warnings.filterwarnings('ignore')
如果你能确定你所针对的 CPU 并指定它,你将获得更好的性能。如果你使用 LLVM,你可以从命令 llc --version 中得到这个信息,以获得 CPU 类型,你可以检查 /proc/cpuinfo,了解你的处理器可能支持的额外扩展。例如,你可以使用 llvm -mcpu=skylake-avx512 来获取带有 AVX-512 指令的 CPU。
tgt = Target(target="llvm", host="llvm")
描述张量计算#
描述矢量加法的计算。TVM 采用了张量语义,每个中间结果都表示为一个多维数组。用户需要描述生成张量的计算规则。首先定义符号变量 n 来表示形状。然后定义两个占位符张量 A 和 B,具有给定的形状 (n,)。然后用 compute 算子来描述结果张量 C。compute 定义了计算,其输出符合指定的张量形状,计算将在张量中的每个位置进行,由 lambda 函数定义。注意,虽然 n 是变量,但它定义了 A、B 和 C 张量之间的一致形状。记住,在这个阶段没有实际的计算发生,因为只是声明了计算应该如何进行。
n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")
Lambda 函数
te.compute 方法的第二个参数是执行计算的函数。在这个例子中,使用一个匿名函数,也被称为 lambda 函数,来定义计算,在本例中是对 A 和 B 的第 i 个元素进行加法。
为计算创建默认的调度#
虽然上面几行描述了计算规则,但可以用许多不同的方式计算 C,以适应不同的设备。对于有多个轴的张量,你可以选择先迭代哪个轴,或者计算可以分成不同的线程。TVM 要求用户提供调度,这是关于计算应该如何进行的描述。TE 中的调度操作可以改变循环顺序,在不同的线程中分割计算,并将数据块分组,以及其他操作。调度背后的重要概念是,它们只描述计算是如何进行的,所以同一个 TE 的不同调度会产生相同的结果。
TVM 允许你创建一个自然的调度,通过以行为单位迭代的方式进行 C 运算。
for (int i = 0; i < n; ++i) {
C[i] = A[i] + B[i];
}
s = te.create_schedule(C.op)
为计算创建默认调度#
有了 TE 表达式和调度,就可以为目标语言和架构(在这里是指 LLVM 和 CPU)生成可运行的代码。向 TVM 提供调度、调度中的 TE 表达式的列表、目标和主机,以及我们要产生的函数的名称。输出的结果是类型消除的(type-erased)函数,可以直接从 Python 中调用。
在下面一行,使用 tvm.build 来创建函数。build 函数需要调度、所需的函数签名(包括输入和输出)以及要编译的目标语言。
fadd = tvm.build(s, [A, B, C], tgt, name="myadd")
运行这个函数,并将其输出与 numpy 中的相同计算进行比较。编译后的 TVM 函数暴露了简洁的 C 语言 API,可以从任何语言调用。首先创建设备,也就是 TVM 可以编译调度的设备(本例中为 CPU)。在本例中,该设备是 LLVM CPU 目标。然后可以初始化设备中的张量,并执行自定义的加法运算。为了验证计算是否正确,我们可以将 c 张量的输出结果与 numpy 进行的相同计算进行比较。
dev = tvm.device(tgt.kind.name, 0)
n = 1024
a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)
b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)
c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)
fadd(a, b, c)
testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())
为了得到这个版本与 numpy 相比有多快的比较,创建辅助函数来运行 TVM 生成代码的配置文件。
import timeit
np_repeat = 100
np_running_time = timeit.timeit(
setup="import numpy\n"
"n = 32768\n"
'dtype = "float32"\n'
"a = numpy.random.rand(n, 1).astype(dtype)\n"
"b = numpy.random.rand(n, 1).astype(dtype)\n",
stmt="answer = a + b",
number=np_repeat,
)
print("Numpy running time: %f" % (np_running_time / np_repeat))
def evaluate_addition(func, target, optimization, log):
dev = tvm.device(target.kind.name, 0)
n = 32768
a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)
b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)
c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)
evaluator = func.time_evaluator(func.entry_name, dev, number=10)
mean_time = evaluator(a, b, c).mean
print("%s: %f" % (optimization, mean_time))
log.append((optimization, mean_time))
log = [("numpy", np_running_time / np_repeat)]
evaluate_addition(fadd, tgt, "naive", log=log)
Numpy running time: 0.000016
naive: 0.000013
更新调度以使用并行#
现在已经说明了 TE 的基本原理,更深入地了解调度的作用,以及如何使用它们来为不同的架构调度张量表达式。调度是一系列应用于表达式的步骤,以多种不同的方式对其进行转换。当调度应用于 TE 中的表达式时,输入和输出保持不变,但在编译时,表达式的实现可以改变。在默认的调度中,这个张量加法是并行运行的,但是很容易在所有的处理器线程中进行并行化。可以将并行调度的操作应用到计算中。
s[C].parallel(C.op.axis[0])
tvm.lower 命令将生成 TE 的中间表示(IR),以及相应的调度。通过在应用不同的调度操作时降低表达式,可以看到调度对计算的顺序的影响。使用旗标 simple_mode=True 来返回一个可读的 C 风格语句。
print(tvm.lower(s, [A, B, C], simple_mode=True))
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [(stride: int32*n: int32)], [], type="auto"),
B: Buffer(B_2: Pointer(float32), float32, [(stride_1: int32*n)], [], type="auto"),
C: Buffer(C_2: Pointer(float32), float32, [(stride_2: int32*n)], [], type="auto")}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [n], [stride], type="auto"), B_1: B_3: Buffer(B_2, float32, [n], [stride_1], type="auto"), C_1: C_3: Buffer(C_2, float32, [n], [stride_2], type="auto")} {
for (i: int32, 0, n) "parallel" {
C[(i*stride_2)] = (A[(i*stride)] + B[(i*stride_1)])
}
}
现在,TVM 有可能在独立的线程上运行这些块。编译并运行这个应用了并行操作的新调度。
fadd_parallel = tvm.build(s, [A, B, C], tgt, name="myadd_parallel")
fadd_parallel(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())
evaluate_addition(fadd_parallel, tgt, "parallel", log=log)
parallel: 0.000022
更新调度以使用矢量化#
现代的 CPU 也有能力对浮点值进行 SIMD 操作,我们可以对我们的计算表达式应用另一个调度,以利用这一优势。实现这一点需要多个步骤:首先,我们必须使用分割调度原语将调度分割成内循环和外循环。内循环可以使用矢量化调度原语来使用 SIMD 指令,然后外循环可以使用并行调度原语来并行化。选择分割因子为你的 CPU 上的线程数。
# 重新创建调度,因为我们用并行操作修改了它
n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")
s = te.create_schedule(C.op)
# 这个 factor 应该被选择来匹配适合你的 CPU 的线程数。
# 这将根据架构的不同而变化,
# 但一个好的规则是将这个 factor 设置为等于可用的 CPU 内核数。
factor = 4
outer, inner = s[C].split(C.op.axis[0], factor=factor)
s[C].parallel(outer)
s[C].vectorize(inner)
fadd_vector = tvm.build(s, [A, B, C], tgt, name="myadd_parallel")
evaluate_addition(fadd_vector, tgt, "vector", log=log)
print(tvm.lower(s, [A, B, C], simple_mode=True))
vector: 0.000017
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [(stride: int32*n: int32)], [], type="auto"),
B: Buffer(B_2: Pointer(float32), float32, [(stride_1: int32*n)], [], type="auto"),
C: Buffer(C_2: Pointer(float32), float32, [(stride_2: int32*n)], [], type="auto")}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [n], [stride], type="auto"), B_1: B_3: Buffer(B_2, float32, [n], [stride_1], type="auto"), C_1: C_3: Buffer(C_2, float32, [n], [stride_2], type="auto")} {
for (i.outer: int32, 0, floordiv((n + 3), 4)) "parallel" {
for (i.inner.s: int32, 0, 4) {
if @tir.likely((((i.outer*4) + i.inner.s) < n), dtype=bool) {
let cse_var_1: int32 = ((i.outer*4) + i.inner.s)
C[(cse_var_1*stride_2)] = (A[(cse_var_1*stride)] + B[(cse_var_1*stride_1)])
}
}
}
}
比较不同的调度#
我们现在可以比较不同的调度:
baseline = log[0][1]
print("%s\t%s\t%s" % ("Operator".rjust(20), "Timing".rjust(20), "Performance".rjust(20)))
for result in log:
print(
"%s\t%s\t%s"
% (result[0].rjust(20), str(result[1]).rjust(20), str(result[1] / baseline).rjust(20))
)
Operator Timing Performance
numpy 1.5522249741479753e-05 1.0
naive 1.3208600000000001e-05 0.8509462365305823
parallel 2.17076e-05 1.3984828463358165
vector 1.6507899999999998e-05 1.0634991882578924
代码特殊化
正如你可能已经注意到的,A、B 和 C 的声明都采取了相同的形状参数 n。TVM 将利用这一点,只向内核传递一个形状参数,正如你在打印的设备代码中发现的那样。这是专业化的一种形式。
在主机端,TVM 会自动生成检查代码,检查参数中的约束。所以如果你把不同形状的数组传入 fadd,就会出现错误。
我们可以做更多的特殊化。例如,我们可以在计算声明中写 n = tvm.runtime.convert(1024),而不是 n = te.var("n") 。生成的函数将只接受长度为 1024 的向量。
我们已经定义、调度并编译了向量加法运算符,然后我们能够在 TVM 运行时上执行它。我们可以将运算符保存为一个库,然后我们可以在以后使用 TVM 运行时加载它。
针对 GPU 的向量加法(可选)#
TVM 能够针对多种架构。在下一个例子中,将针对 GPU 的向量加法进行编译。
# 如果你想运行这段代码,改变 ``run_cuda = True``。
# 注意,在默认情况下,这个例子不会在 docs CI 中运行。
run_cuda = True
if run_cuda:
# Change this target to the correct backend for you gpu. For example: cuda (NVIDIA GPUs),
# rocm (Radeon GPUS), OpenCL (opencl).
tgt_gpu = tvm.target.Target(target="cuda", host="llvm")
# Recreate the schedule
n = te.var("n")
A = te.placeholder((n,), name="A")
B = te.placeholder((n,), name="B")
C = te.compute(A.shape, lambda i: A[i] + B[i], name="C")
print(type(C))
s = te.create_schedule(C.op)
bx, tx = s[C].split(C.op.axis[0], factor=64)
################################################################################
# Finally we must bind the iteration axis bx and tx to threads in the GPU
# compute grid. The naive schedule is not valid for GPUs, and these are
# specific constructs that allow us to generate code that runs on a GPU.
s[C].bind(bx, te.thread_axis("blockIdx.x"))
s[C].bind(tx, te.thread_axis("threadIdx.x"))
######################################################################
# Compilation
# -----------
# After we have finished specifying the schedule, we can compile it
# into a TVM function. By default TVM compiles into a type-erased
# function that can be directly called from the python side.
#
# In the following line, we use tvm.build to create a function.
# The build function takes the schedule, the desired signature of the
# function (including the inputs and outputs) as well as target language
# we want to compile to.
#
# The result of compilation fadd is a GPU device function (if GPU is
# involved) as well as a host wrapper that calls into the GPU
# function. fadd is the generated host wrapper function, it contains
# a reference to the generated device function internally.
fadd = tvm.build(s, [A, B, C], target=tgt_gpu, name="myadd")
################################################################################
# The compiled TVM function exposes a concise C API that can be invoked from
# any language.
#
# We provide a minimal array API in python to aid quick testing and prototyping.
# The array API is based on the `DLPack <https://github.com/dmlc/dlpack>`_ standard.
#
# - We first create a GPU device.
# - Then tvm.nd.array copies the data to the GPU.
# - ``fadd`` runs the actual computation
# - ``numpy()`` copies the GPU array back to the CPU (so we can verify correctness).
#
# Note that copying the data to and from the memory on the GPU is a required step.
dev = tvm.device(tgt_gpu.kind.name, 0)
n = 1024
a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)
b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)
c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)
fadd(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())
################################################################################
# Inspect the Generated GPU Code
# ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
# You can inspect the generated code in TVM. The result of tvm.build is a TVM
# Module. fadd is the host module that contains the host wrapper, it also
# contains a device module for the CUDA (GPU) function.
#
# The following code fetches the device module and prints the content code.
if (
tgt_gpu.kind.name == "cuda"
or tgt_gpu.kind.name == "rocm"
or tgt_gpu.kind.name.startswith("opencl")
):
dev_module = fadd.imported_modules[0]
print("-----GPU code-----")
print(dev_module.get_source())
else:
print(fadd.get_source())
<class 'tvm.te.tensor.Tensor'>
-----GPU code-----
#ifdef _WIN32
using uint = unsigned int;
using uchar = unsigned char;
using ushort = unsigned short;
using int64_t = long long;
using uint64_t = unsigned long long;
#else
#define uint unsigned int
#define uchar unsigned char
#define ushort unsigned short
#define int64_t long long
#define uint64_t unsigned long long
#endif
extern "C" __global__ void __launch_bounds__(64) myadd_kernel0(float* __restrict__ C, float* __restrict__ A, float* __restrict__ B, int n, int stride, int stride1, int stride2) {
if (((int)blockIdx.x) < (n >> 6)) {
C[(((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) * stride)] = (A[(((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) * stride1)] + B[(((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) * stride2)]);
} else {
if (((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) < n) {
C[(((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) * stride)] = (A[(((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) * stride1)] + B[(((((int)blockIdx.x) * 64) + ((int)threadIdx.x)) * stride2)]);
}
}
}
保存和加载已编译的模块#
除了运行时编译,我们还可以将编译后的模块保存到文件中,以后再加载回来。
下面的代码首先执行了以下步骤:
它将编译后的主机模块保存到一个对象文件中。
然后它将设备模块保存到 ptx 文件中。
cc.create_shared调用编译器(gcc)来创建共享库
from tvm.contrib import cc
from tvm.contrib import utils
temp = utils.tempdir()
fadd.save(temp.relpath("myadd.o"))
if tgt.kind.name == "cuda":
fadd.imported_modules[0].save(temp.relpath("myadd.ptx"))
if tgt.kind.name == "rocm":
fadd.imported_modules[0].save(temp.relpath("myadd.hsaco"))
if tgt.kind.name.startswith("opencl"):
fadd.imported_modules[0].save(temp.relpath("myadd.cl"))
cc.create_shared(temp.relpath("myadd.so"), [temp.relpath("myadd.o")])
print(temp.listdir())
['myadd.so', 'myadd.o']
模块存储格式
CPU(主机)模块被直接保存为共享库(.so)。设备代码可以有多种自定义格式。在我们的例子中,设备代码被保存在 ptx 中,还有一个元数据 json 文件。它们可以通过导入分离加载和链接。
加载已编译的模块#
我们可以从文件系统中加载编译好的模块并运行代码。下面的代码分别加载主机和设备模块,并将它们链接在一起。我们可以验证新加载的功能是否工作。
fadd1 = tvm.runtime.load_module(temp.relpath("myadd.so"))
if tgt.kind.name == "cuda":
fadd1_dev = tvm.runtime.load_module(temp.relpath("myadd.ptx"))
fadd1.import_module(fadd1_dev)
if tgt.kind.name == "rocm":
fadd1_dev = tvm.runtime.load_module(temp.relpath("myadd.hsaco"))
fadd1.import_module(fadd1_dev)
if tgt.kind.name.startswith("opencl"):
fadd1_dev = tvm.runtime.load_module(temp.relpath("myadd.cl"))
fadd1.import_module(fadd1_dev)
fadd1(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())
把所有东西都装进库#
在上面的例子中,分别存储了设备和主机代码。TVM 也支持将所有东西作为共享库导出。在底层,将设备模块打包成二进制的 blob,并将它们与主机代码连接在一起。目前支持打包 Metal、OpenCL 和 CUDA 模块。
fadd.export_library(temp.relpath("myadd_pack.so"))
fadd2 = tvm.runtime.load_module(temp.relpath("myadd_pack.so"))
fadd2(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())
运行时 API 和线程安全
TVM 的编译模块并不依赖于 TVM 编译器。相反,它们只依赖于一个最小的运行时库。TVM 运行库包装了设备驱动程序,并提供线程安全和设备无关的调用到编译的函数。
这意味着你可以从任何线程、任何 GPU 上调用已编译的 TVM 函数,只要你已经为该 GPU 编译了代码。
生成 OpenCL 代码#
TVM 提供代码生成功能到多个后端。我们还可以生成 OpenCL 代码或 LLVM 代码,在 CPU 后端运行。
下面的代码块生成 OpenCL 代码,在 OpenCL 设备上创建阵列,并验证代码的正确性。
if tgt.kind.name.startswith("opencl"):
fadd_cl = tvm.build(s, [A, B, C], tgt, name="myadd")
print("------opencl code------")
print(fadd_cl.imported_modules[0].get_source())
dev = tvm.cl(0)
n = 1024
a = tvm.nd.array(np.random.uniform(size=n).astype(A.dtype), dev)
b = tvm.nd.array(np.random.uniform(size=n).astype(B.dtype), dev)
c = tvm.nd.array(np.zeros(n, dtype=C.dtype), dev)
fadd_cl(a, b, c)
tvm.testing.assert_allclose(c.numpy(), a.numpy() + b.numpy())
TE 调度原语
TVM 包括一些不同的调度原语:
split:将一个指定的轴按定义的因子(factor)分成两个轴。tile:将一个计算按定义的 factor 分成两个轴。fuse:融合一个计算的两个连续轴。reorder:可以将一个计算的轴重新排序到一个定义的顺序。bind:可以将一个计算绑定到一个特定的线程,在GPU编程中很有用。compute_at:默认情况下,TVM 会在函数的最外层计算张量,也就是默认的根。compute_at指定一个张量应该在另一个运算符的第一个计算轴上计算。compute_inline:当标记为内联时,一个计算将被展开,然后插入到需要张量的地址中。compute_root:将一个计算移到函数的最外层,或根部。这意味着该阶段的计算将在进入下一阶段之前被完全计算。
这些原语的完整描述可以在 调度原语 文档页中找到。
实例2:用 TE 手动优化矩阵乘法#
现在我们将考虑第二个更高级的例子,演示仅用 18 行 python 代码,TVM 如何将一个普通的矩阵乘法操作加快 18 倍。
矩阵乘法是计算密集型运算。为了获得良好的 CPU 性能,有两个重要的优化措施:
提高内存访问的高速缓存命中率。复杂的数值计算和热点内存(hot-spot memory)访问都可以通过高缓存命中率(high cache hit rate)来加速。这就要求我们将原点内存(origin )访问模式转化为符合高速缓存策略的模式。
SIMD(单指令多数据),也被称为矢量处理单元。在每个周期中,SIMD 可以处理一小批数据,而不是处理一个单一的值。这就要求我们将循环体中的数据访问模式转化为统一模式,以便 LLVM 后端可以将其降低到 SIMD。
本教程中使用的技术是 资源库 中提到的技巧的一个子集。其中一些已经被 TVM 抽象自动应用了,但由于 TVM 的限制,其中一些不能自动应用。
准备和性能基线#
我们首先收集 numpy 实现矩阵乘法的性能数据。
import tvm
import tvm.testing
from tvm import te
import numpy
# The size of the matrix
# (M, K) x (K, N)
# You are free to try out different shapes, sometimes TVM optimization outperforms numpy with MKL.
M = 1024
K = 1024
N = 1024
# The default tensor data type in tvm
dtype = "float32"
# You will want to adjust the target to match any CPU vector extensions you
# might have. For example, if you're using using Intel AVX2 (Advanced Vector
# Extensions) ISA for SIMD, you can get the best performance by changing the
# following line to ``llvm -mcpu=core-avx2``, or specific type of CPU you use.
# Recall that you're using llvm, you can get this information from the command
# ``llc --version`` to get the CPU type, and you can check ``/proc/cpuinfo``
# for additional extensions that your processor might support.
target = tvm.target.Target(target="llvm", host="llvm")
dev = tvm.device(target.kind.name, 0)
# Random generated tensor for testing
a = tvm.nd.array(numpy.random.rand(M, K).astype(dtype), dev)
b = tvm.nd.array(numpy.random.rand(K, N).astype(dtype), dev)
# Repeatedly perform a matrix multiplication to get a performance baseline
# for the default numpy implementation
np_repeat = 100
np_running_time = timeit.timeit(
setup="import numpy\n"
"M = " + str(M) + "\n"
"K = " + str(K) + "\n"
"N = " + str(N) + "\n"
'dtype = "float32"\n'
"a = numpy.random.rand(M, K).astype(dtype)\n"
"b = numpy.random.rand(K, N).astype(dtype)\n",
stmt="answer = numpy.dot(a, b)",
number=np_repeat,
)
print("Numpy running time: %f" % (np_running_time / np_repeat))
answer = numpy.dot(a.numpy(), b.numpy())
Numpy running time: 0.023805
现在用 TVM TE 编写基本的矩阵乘法,并验证它产生的结果与 numpy 的实现相同。我们还写了一个函数,它将帮助衡量调度优化的性能。
# TVM Matrix Multiplication using TE
k = te.reduce_axis((0, K), "k")
A = te.placeholder((M, K), name="A")
B = te.placeholder((K, N), name="B")
C = te.compute((M, N), lambda x, y: te.sum(A[x, k] * B[k, y], axis=k), name="C")
# Default schedule
s = te.create_schedule(C.op)
func = tvm.build(s, [A, B, C], target=target, name="mmult")
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), dev)
func(a, b, c)
tvm.testing.assert_allclose(c.numpy(), answer, rtol=1e-5)
def evaluate_operation(s, vars, target, name, optimization, log):
func = tvm.build(s, [A, B, C], target=target, name="mmult")
assert func
c = tvm.nd.array(numpy.zeros((M, N), dtype=dtype), dev)
func(a, b, c)
tvm.testing.assert_allclose(c.numpy(), answer, rtol=1e-5)
evaluator = func.time_evaluator(func.entry_name, dev, number=10)
mean_time = evaluator(a, b, c).mean
print("%s: %f" % (optimization, mean_time))
log.append((optimization, mean_time))
log = []
evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="none", log=log)
none: 2.233156
让我们来看看使用 TVM 低级函数的运算器和默认调度的中间表示。请注意这个实现基本上是矩阵乘法的天真实现,在 A 和 B 矩阵的索引上使用三个嵌套循环。
print(tvm.lower(s, [A, B, C], simple_mode=True))
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
for (x: int32, 0, 1024) {
for (y: int32, 0, 1024) {
C[((x*1024) + y)] = 0f32
for (k: int32, 0, 1024) {
let cse_var_2: int32 = (x*1024)
let cse_var_1: int32 = (cse_var_2 + y)
C[cse_var_1] = (C[cse_var_1] + (A[(cse_var_2 + k)]*B[((k*1024) + y)]))
}
}
}
}
优化1:阻塞#
提高缓冲区命中率的一个重要技巧是阻塞,在这个过程中,你的内存访问结构是在一个块的内部有一个小的邻域,具有很高的内存定位性。在本教程中,我们选择一个 32 的块因子。这将导致一个块充满 32 * 32 * sizeof(float) 的内存区域。这相当于一个 4KB 的缓存大小,而 L1 缓存的参考缓存大小为 32KB。
我们首先为 C 操作创建一个默认的调度,然后用指定的块因子对其应用一个 tile 调度原语,调度原语返回所产生的循环顺序,从最外层到最内层,作为一个向量 [x_outer, y_outer, x_inner, y_inner]。然后我们得到操作输出的还原轴,并使用 4 的因子对其进行分割操作。这个因子并不直接影响我们现在正在进行的阻塞优化,但在以后我们应用矢量化时将会很有用。
现在操作已经被阻塞了,我们可以重新调度计算的顺序,把减少操作放到计算的最外层循环中,帮助保证被阻止的数据仍然在缓存中。这样就完成了调度,我们可以建立并测试与原生的调度相比的性能。
bn = 32
# Blocking by loop tiling
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
# Hoist reduction domain outside the blocking loop
s[C].reorder(xo, yo, ko, ki, xi, yi)
evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="blocking", log=log)
blocking: 0.249289
通过重新安排计算顺序以利用缓存,你应该看到计算的性能有了明显的改善。现在,打印内部表示,并将其与原始表示进行比较。
print(tvm.lower(s, [A, B, C], simple_mode=True))
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
for (x.outer: int32, 0, 32) {
for (y.outer: int32, 0, 32) {
for (x.inner.init: int32, 0, 32) {
for (y.inner.init: int32, 0, 32) {
C[((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)) + y.inner.init)] = 0f32
}
}
for (k.outer: int32, 0, 256) {
for (k.inner: int32, 0, 4) {
for (x.inner: int32, 0, 32) {
for (y.inner: int32, 0, 32) {
let cse_var_3: int32 = (y.outer*32)
let cse_var_2: int32 = ((x.outer*32768) + (x.inner*1024))
let cse_var_1: int32 = ((cse_var_2 + cse_var_3) + y.inner)
C[cse_var_1] = (C[cse_var_1] + (A[((cse_var_2 + (k.outer*4)) + k.inner)]*B[((((k.outer*4096) + (k.inner*1024)) + cse_var_3) + y.inner)]))
}
}
}
}
}
}
}
优化 2: 矢量化#
另一个重要的优化技巧是矢量化。当内存访问模式是统一的,编译器可以检测到这种模式并将连续的内存传递给 SIMD 矢量处理器。在 TVM 中,我们可以使用 vectorize 接口来提示编译器这种模式,利用这一硬件特性。
在本教程中,我们选择对内循环的行数据进行矢量化,因为在我们之前的优化中,它已经是缓存友好的。
# Apply the vectorization optimization
s[C].vectorize(yi)
evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="vectorization", log=log)
# The generalized IR after vectorization
print(tvm.lower(s, [A, B, C], simple_mode=True))
vectorization: 0.257297
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
for (x.outer: int32, 0, 32) {
for (y.outer: int32, 0, 32) {
for (x.inner.init: int32, 0, 32) {
C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)
}
for (k.outer: int32, 0, 256) {
for (k.inner: int32, 0, 4) {
for (x.inner: int32, 0, 32) {
let cse_var_3: int32 = (y.outer*32)
let cse_var_2: int32 = ((x.outer*32768) + (x.inner*1024))
let cse_var_1: int32 = (cse_var_2 + cse_var_3)
C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1, 1, 32)] + (broadcast(A[((cse_var_2 + (k.outer*4)) + k.inner)], 32)*B[ramp((((k.outer*4096) + (k.inner*1024)) + cse_var_3), 1, 32)]))
}
}
}
}
}
}
优化3:循环交换#
如果我们看一下上面的 IR,我们可以看到内循环的行数据被矢量化,B 被转化为 PackedB(这从内循环的 (float32x32*)B2 部分可以看出)。现在 PackedB 的遍历是顺序的。所以我们要看一下 A 的访问模式。在当前的计划中,A 是被逐列访问的,这对缓冲区不友好。如果我们改变 ki 和内轴 xi 的嵌套循环顺序,A 矩阵的访问模式将对缓存更友好。
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
# re-ordering
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)
evaluate_operation(
s, [A, B, C], target=target, name="mmult", optimization="loop permutation", log=log
)
# Again, print the new generalized IR
print(tvm.lower(s, [A, B, C], simple_mode=True))
loop permutation: 0.130006
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
for (x.outer: int32, 0, 32) {
for (y.outer: int32, 0, 32) {
for (x.inner.init: int32, 0, 32) {
C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)
}
for (k.outer: int32, 0, 256) {
for (x.inner: int32, 0, 32) {
for (k.inner: int32, 0, 4) {
let cse_var_3: int32 = (y.outer*32)
let cse_var_2: int32 = ((x.outer*32768) + (x.inner*1024))
let cse_var_1: int32 = (cse_var_2 + cse_var_3)
C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1, 1, 32)] + (broadcast(A[((cse_var_2 + (k.outer*4)) + k.inner)], 32)*B[ramp((((k.outer*4096) + (k.inner*1024)) + cse_var_3), 1, 32)]))
}
}
}
}
}
}
优化4:数组打包#
另一个重要的技巧是数组打包。这个技巧是对数组的存储维度进行重新排序,将某些维度上的连续访问模式转换为扁平化后的顺序模式。
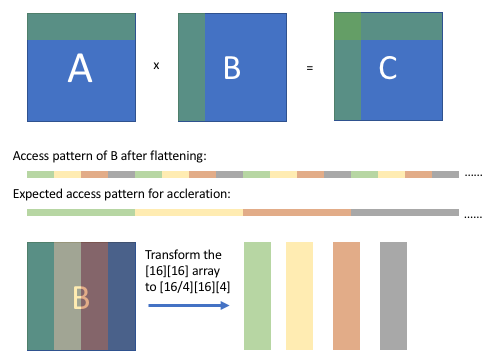
正如上图所示,在阻塞计算后,我们可以观察到 B 的数组访问模式(扁平化后),它是有规律的,但是不连续的。我们期望经过一些转换后,我们可以得到一个连续的访问模式。通过将 [16][16] 数组重新排序为 [16/4][16][4] 数组,当从打包的数组中抓取相应的值时,B 的访问模式将是连续的。
为了实现这一目标,将不得不从新的默认调度开始,考虑到 B 的新包装,值得花点时间来评论一下。TE 是编写优化运算符的强大而富有表现力的语言,但它往往需要对你所编写的底层算法、数据结构和硬件目标有一些了解。在本教程的后面,我们将讨论一些让 TVM 承担这一负担的选项。无论如何,让我们继续编写新的优化调度。
# 必须重写算法。
packedB = te.compute((N / bn, K, bn), lambda x, y, z: B[y, x * bn + z], name="packedB")
C = te.compute(
(M, N),
lambda x, y: te.sum(A[x, k] * packedB[y // bn, k, tvm.tir.indexmod(y, bn)], axis=k),
name="C",
)
s = te.create_schedule(C.op)
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
(k,) = s[C].op.reduce_axis
ko, ki = s[C].split(k, factor=4)
s[C].reorder(xo, yo, ko, xi, ki, yi)
s[C].vectorize(yi)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="array packing", log=log)
# Here is the generated IR after array packing.
print(tvm.lower(s, [A, B, C], simple_mode=True))
array packing: 0.140257
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {
for (x: int32, 0, 32) "parallel" {
for (y: int32, 0, 1024) {
packedB_1: Buffer(packedB, float32x32, [32768], [])[((x*1024) + y)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
}
}
for (x.outer: int32, 0, 32) {
for (y.outer: int32, 0, 32) {
for (x.inner.init: int32, 0, 32) {
C[ramp((((x.outer*32768) + (x.inner.init*1024)) + (y.outer*32)), 1, 32)] = broadcast(0f32, 32)
}
for (k.outer: int32, 0, 256) {
for (x.inner: int32, 0, 32) {
for (k.inner: int32, 0, 4) {
let cse_var_3: int32 = ((x.outer*32768) + (x.inner*1024))
let cse_var_2: int32 = (k.outer*4)
let cse_var_1: int32 = (cse_var_3 + (y.outer*32))
C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1, 1, 32)] + (broadcast(A[((cse_var_3 + cse_var_2) + k.inner)], 32)*packedB_1[(((y.outer*1024) + cse_var_2) + k.inner)]))
}
}
}
}
}
}
}
优化 5:通过缓存优化块的写入#
到目前为止,我们所有的优化都集中在有效地访问和计算 A 和 B 矩阵的数据以计算 C 矩阵上。在阻塞优化之后,运算器将逐块地将结果写入 C,而且访问模式不是顺序的。我们可以通过使用一个顺序缓存数组来解决这个问题,使用 cache_write、compute_at 和 unroll 的组合来保存块结果,并在所有块结果准备好后写入 C。
s = te.create_schedule(C.op)
# Allocate write cache
CC = s.cache_write(C, "global")
xo, yo, xi, yi = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
# Write cache is computed at yo
s[CC].compute_at(s[C], yo)
# New inner axes
xc, yc = s[CC].op.axis
(k,) = s[CC].op.reduce_axis
ko, ki = s[CC].split(k, factor=4)
s[CC].reorder(ko, xc, ki, yc)
s[CC].unroll(ki)
s[CC].vectorize(yc)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
evaluate_operation(s, [A, B, C], target=target, name="mmult", optimization="block caching", log=log)
# Here is the generated IR after write cache blocking.
print(tvm.lower(s, [A, B, C], simple_mode=True))
block caching: 0.131626
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global;
allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global {
for (x: int32, 0, 32) "parallel" {
for (y: int32, 0, 1024) {
packedB_1: Buffer(packedB, float32x32, [32768], [])[((x*1024) + y)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
}
}
for (x.outer: int32, 0, 32) {
for (y.outer: int32, 0, 32) {
for (x.c.init: int32, 0, 32) {
C.global_1: Buffer(C.global, float32, [1024], [])[ramp((x.c.init*32), 1, 32)] = broadcast(0f32, 32)
}
for (k.outer: int32, 0, 256) {
for (x.c: int32, 0, 32) {
let cse_var_4: int32 = (k.outer*4)
let cse_var_3: int32 = (x.c*32)
let cse_var_2: int32 = ((y.outer*1024) + cse_var_4)
let cse_var_1: int32 = (((x.outer*32768) + (x.c*1024)) + cse_var_4)
{
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[cse_var_1], 32)*packedB_1[cse_var_2]))
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 1)], 32)*packedB_1[(cse_var_2 + 1)]))
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 2)], 32)*packedB_1[(cse_var_2 + 2)]))
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 3)], 32)*packedB_1[(cse_var_2 + 3)]))
}
}
}
for (x.inner: int32, 0, 32) {
for (y.inner: int32, 0, 32) {
C[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = C.global_1[((x.inner*32) + y.inner)]
}
}
}
}
}
}
优化6:并行化#
到目前为止,我们的计算只被设计为使用单核。几乎所有的现代处理器都有多个内核,计算可以从并行运行的计算中获益。最后的优化是利用线程级并行化的优势。
# parallel
s[C].parallel(xo)
x, y, z = s[packedB].op.axis
s[packedB].vectorize(z)
s[packedB].parallel(x)
evaluate_operation(
s, [A, B, C], target=target, name="mmult", optimization="parallelization", log=log
)
# Here is the generated IR after parallelization.
print(tvm.lower(s, [A, B, C], simple_mode=True))
parallelization: 0.026403
@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
buffer_map = {A_1: A, B_1: B, C_1: C}
preflattened_buffer_map = {A_1: A_3: Buffer(A_2, float32, [1024, 1024], []), B_1: B_3: Buffer(B_2, float32, [1024, 1024], []), C_1: C_3: Buffer(C_2, float32, [1024, 1024], [])} {
allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {
for (x: int32, 0, 32) "parallel" {
for (y: int32, 0, 1024) {
packedB_1: Buffer(packedB, float32x32, [32768], [])[((x*1024) + y)] = B[ramp(((y*1024) + (x*32)), 1, 32)]
}
}
for (x.outer: int32, 0, 32) "parallel" {
allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global;
for (y.outer: int32, 0, 32) {
for (x.c.init: int32, 0, 32) {
C.global_1: Buffer(C.global, float32, [1024], [])[ramp((x.c.init*32), 1, 32)] = broadcast(0f32, 32)
}
for (k.outer: int32, 0, 256) {
for (x.c: int32, 0, 32) {
let cse_var_4: int32 = (k.outer*4)
let cse_var_3: int32 = (x.c*32)
let cse_var_2: int32 = ((y.outer*1024) + cse_var_4)
let cse_var_1: int32 = (((x.outer*32768) + (x.c*1024)) + cse_var_4)
{
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[cse_var_1], 32)*packedB_1[cse_var_2]))
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 1)], 32)*packedB_1[(cse_var_2 + 1)]))
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 2)], 32)*packedB_1[(cse_var_2 + 2)]))
C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 3)], 32)*packedB_1[(cse_var_2 + 3)]))
}
}
}
for (x.inner: int32, 0, 32) {
for (y.inner: int32, 0, 32) {
C[((((x.outer*32768) + (x.inner*1024)) + (y.outer*32)) + y.inner)] = C.global_1[((x.inner*32) + y.inner)]
}
}
}
}
}
}
矩阵乘法实例总结#
在应用了上述仅有 18 行代码的简单优化后,我们生成的代码可以开始接近 numpy 与 Math Kernel Library(MKL)的性能。由于我们在工作中一直在记录性能,所以我们可以比较一下结果。
baseline = log[0][1]
print("%s\t%s\t%s" % ("Operator".rjust(20), "Timing".rjust(20), "Performance".rjust(20)))
for result in log:
print(
"%s\t%s\t%s"
% (result[0].rjust(20), str(result[1]).rjust(20), str(result[1] / baseline).rjust(20))
)
Operator Timing Performance
none 2.233155965 1.0
blocking 0.2492886151 0.11163063351018566
vectorization 0.257297356 0.1152169217164373
loop permutation 0.1300062278 0.058216367256731225
array packing 0.140256607 0.06280645382509144
block caching 0.13162604679999998 0.05894171695258194
parallelization 0.026402827 0.011823100318029064
请注意,网页上的输出反映了在一个非独家 Docker 容器上的运行时间,应该被认为是不可靠的。强烈建议你自己运行该教程,观察 TVM 取得的性能提升,并仔细研究每个例子,了解对矩阵乘法操作的迭代改进。
最后说明和总结#
如前所述,如何使用 TE 和调度原语进行优化,可能需要对底层架构和算法有一些了解。然而,TE 的设计是作为更复杂的算法的基础,可以搜索潜在的优化。有了这篇关于 TE 的介绍中的知识,我们现在可以开始探索 TVM 如何将调度优化过程自动化。
本教程提供了一个 TVM 张量表达(TE)工作流程的演练,使用了一个矢量添加和一个矩阵乘法的例子。一般的工作流程是:
通过一系列的操作来描述你的计算。
描述我们要如何计算使用调度原语。
编译到我们想要的目标函数。
可以选择保存该函数以便以后加载。
即将出版的教程扩展了矩阵乘法的例子,并展示了你如何建立矩阵乘法和其他操作的通用模板,这些模板具有可调整的参数,允许你为特定平台自动优化计算。